Planck length, minimal length?
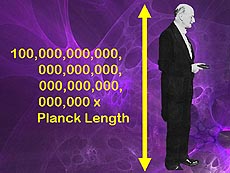 |
In this image of Max Planck, we see that the length of Planck is 1035 Planck lengths.
|
Read the complete column on Planck length.
We received an email from Bill G., an inquisitive reader:
"It is said that the Planck length is the smallest length possible. Is that true? If so, why?"
Readers should be warned that this article is a little more complicated than usual. Simple questions sometimes require detailed answers.
First, let's talk about what Planck length is. In 1899, German physicist Max Planck proposed a universal set of units for length, time, mass, temperature and other physical qualities. He was trying to come up with a way to define units that depended only on constants of the universe. To get an idea of why this is important, think about the difficulties associated with expressing lengths in meters versus feet. It would be even worse if we were talking to some Martian scientists and trying to compare our lengths to theirs.
A modern treatment of Planck's work begins with the speed of light c, gravitational constant G, reduced Planck constant ħ, Coulomb constant k and Boltzmann constant kB. By taking different combinations of these variables, one can find Planck units, which are truly universal. For instance, by taking √
ħG/c3 , one gets a length. This length is the Planck length, and it is 1.6 x 10-35 meters.
The beauty of the Planck units in general and the Planck length in particular is that no matter what units one chooses to make measurements, be it English, metric or Martian, everyone will determine the same Planck length. Planck himself said in his paper to the Prussian Academy of Sciences, "These necessarily retain their meaning for all times and for all civilizations, even extraterrestrial and non-human ones, and can therefore be designated as 'natural units.'"
Now that we understand what Planck length is, we can turn our attention to the question of whether it is the smallest possible length. For that, we need to turn to quantum mechanics and, specifically, a thing called the Heisenberg uncertainty principle. This general principle of the universe states that it is impossible to measure position and momentum simultaneously with infinite precision — measure one well and the other will be measured poorly.
In 1964, C. Alden Mead published a paper in which he determined the effect of gravity on a phenomenon called diffraction, which describes what happens to light when you send it through a small aperture. Because gravity is so incredibly weak compared to the force that governs the behavior of light (the electromagnetic force), its effect is completely ignored in diffraction calculations. But Mead was curious about quantifying gravity's negligible effect. When you scatter a particle of light off another particle — say an atom — the atom's gravitational attraction to the light particle causes an intrinsic uncertainty in the atom's location. Mead used the uncertainty principle and the gravitational effect of the photon to show that it is impossible to determine the position of an object to a precision smaller than the Planck length.
Read more
—Don Lincoln
Want a phrase defined? Have a question? Email today@fnal.gov.
|